cross validation, KNN, SVM, DecisionTree, NaiveBayes, 앙상블 기법, 비지도 학습
K-폴드 교차 검증(K-fold cross validation)
- 학습 데이터의 일정 부분을 검증데이터로 쓰되, n번의 검증 과정을 통해 학습 데이터의 모든 데이터를 한 번씩 검증데이터로 사용하는 방식
- Training Set, Validation Set, Test Set의 개념 구분
장점
- 검증 결과가 일정 데이터에 치우치지 않고 모든 데이터에 대한 결과이므로 신빙성이 높음
- 별도로 검증 데이터를 분리하지 않아도 됨

K-Nearest Neighbor(K-NN)
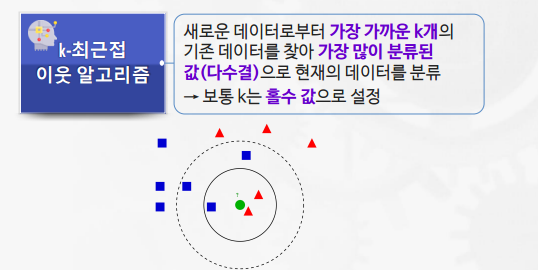
- k가 너무 작으면 overfitting, k가 너무 크면 underfitting 위험이 있다.
- kNN 알고리즘은 다중 분류에도 탁월한 성능을 보인다
장점
- 원리가 간단하여 구현하기 쉬움
- 수치 기반 데이터 분류에 높은 성능
- 별도의 학습 모델이 필요 없음
단점
- 예측 속도가 느림
- 고차원 데이터 처리를 위해 차원 축소가 필요
- k 값 선정에 따라 성능이 좌우
SVM(Support Vector Machine)
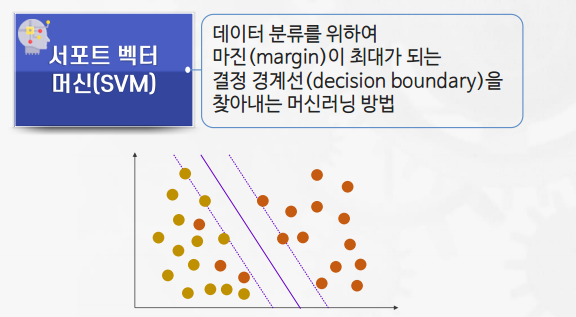
주요 용어
- 결정 경계선(decision boundary): 서로 다른 분류 값을 결정하는 경계
- 서포트 벡터(support vector): 결정 경계선과 가장 가까이 맞닿은 데이터 포인트
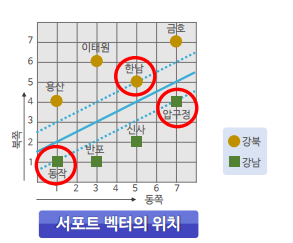
- 마진(margin): 서포트 벡터와 결정 경계 사이의 거리
- 비용(cost): 얼마나 많은 데이터 샘플이 다른 클래스에 놓이는 것을 허용하는지 결정
- 낮을수록, 마진을 최대한 높이고 학습에러율을 증가시키는 방향으로 결정 경계선 만듦
- 높을수록, 마진은 작아지고 학습 에러율은 감소하는 방향으로 결정 경계선 만듦
- 비용이 너무 낮으면 과소적합, 너무 높으면 과대적합의 위험성 존재
- 커널 트릭(Kernel Trick): 실제로 데이터를 고차원으로 보내진 않지만 보낸 것과 동일한 효과를 줘서 매우 빠른 속도로 결정 경계선을 찾는 방법
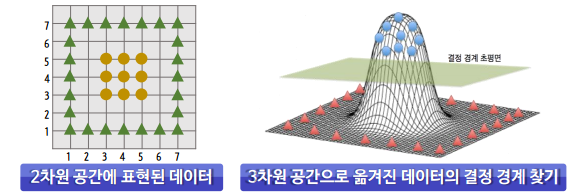
장점
- 특성이 다양한 데이터 분류에 강함
- 파라미터를 조정해서 과대/과소적합에 대응 가능
- 적은 학습 데이터로도 정확도가 높은 분류 성능
단점
- 데이터 전처리 과정이 매우 중요
- 특성이 많을 경우, 결정 경계 및 데이터의 시각화가 어려움
의사결정트리(Decision Tree)
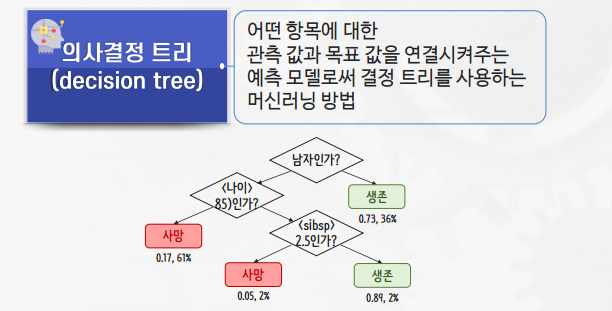
의사결정 트리의 핵심
- 영향력이 큰 특징을 상위 노드로, 영향력이 작은 특징은 하위 노드로 선택하는 것
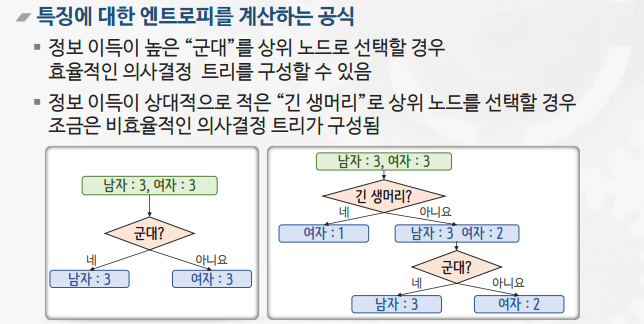
- 의사결정 트리는 특징 별 영향력의 크고 작음을 비교하기 위해 다음과 같은 두 가지 방법 중 하나를 사용함
- 엔트로피
약간의 정보를 획득하는 과정은 정답에 대한 불 확실성이 줄어든다는 것.






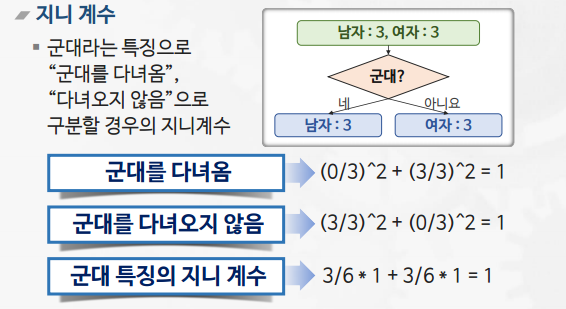
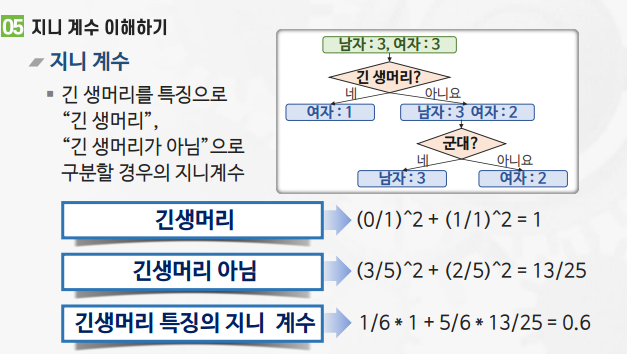
- 지니 계수
- 불순도를 측정하는 지표
- 사이킷런의 의사결정 트리는 CART 타입의 트리(이진 분류)


의사결정트리 알고리즘의 장단점
장점
- 수학적인 지식이 없어도 결과를 해석하고 이해하기 쉬움
- 수치 데이터 및 범주 데이터에 모두 사용 가능
- 정확도가 비교적 높은편
단점
- 과대적합의 위험성이 높음
- 최적의 솔루션을 보장하지 않음
나이브 베이즈 분류기(Naive Bayes Classifier)

다항 분포 나이브 베이즈(Multinomial Naïve Bayes)
- 데이터의 특징이 출현 횟수로 표현되었을 때 사용
- 예) 주사위를 10번 던졌을 때, 1이 한 번, 2가 두 번, 3이 세 번, 4가 네 번 나왔을 경우, (1,2,3,4,0,0)으로 나타남
베르누이 나이브 베이즈 모델(Bernoulli Naïve Bayes)
- 데이터의 특징이 0 또는 1로 표현되었을 때 사용
- 예) 주사위를 10번 던졌을 때, 1이 한 번, 2가 두 번, 3이 세 번, 4가 네 번 나왔을 경우, (1,1,1,1,0,0)으로 나타남
스무딩: 학습 데이터에 없던 데이터가 출현해도 빈도수에 1을 더해서 확률이 0이 되는 현상을 방지
나이브 베이즈 알고리즘의 장단점
장점
- 실전에서 높은 정확도
- 문서 분류 및 스팸 메일 분류에 강함
- 계산 속도가 다른 모델들에 비해 상당히 빠름
단점
- 모든 데이터의 특징을 독립적인 사건이라고 가정하는 것은 문서 분류에 적합할지는 모르나 다른 분류 모델에는 제약이 될 수 있음
앙상블 기법
여러 개의 분류기를 생성하고, 그 예측을 결합하여 더욱 정확한 예측을 도출하는 기법
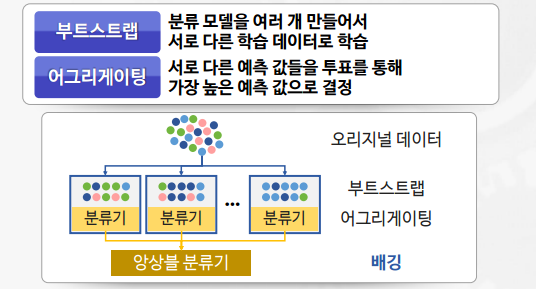
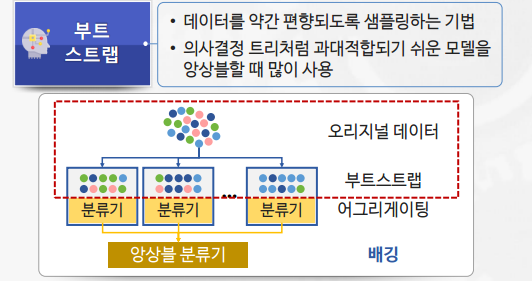
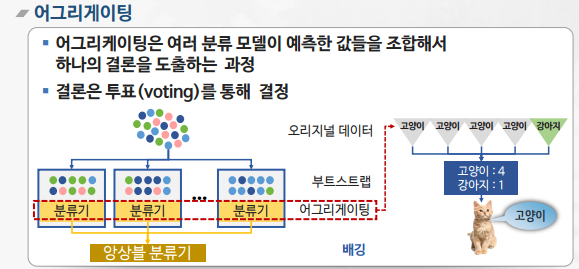
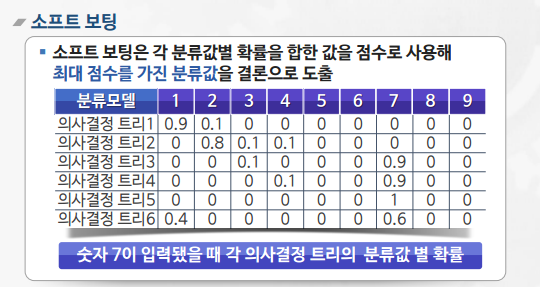
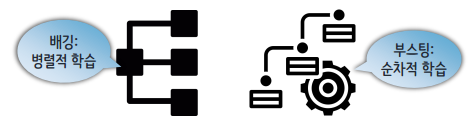
배깅(Bagging)

- 알고리즘의 안정성 및 정확성 향상을 위해 수행
- 부트스트랩(bootstrap)과 어그리게이팅(aggregating)을 합친 단어
- 대표적인 모델 : 랜덤포레스트(Random Forest)



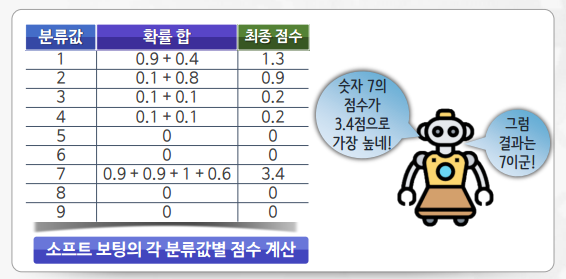
랜덤포레스트(Random Forest)
- 다수의 결정 트리들을 배깅해서 예측을 실행하는 앙상블 기법
- 각 노드에 주어진 데이터를 샘플링해서 일부 데이터를 제외한 채, 최적의 특징을 찾아 트리를 분기
- 모델의 편향을 증가시켜 과대적합의 위험을 감소
- 다양한 분야에서 비교적 좋은 성능을 보여줌
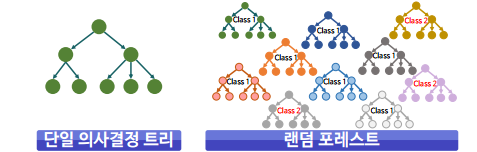
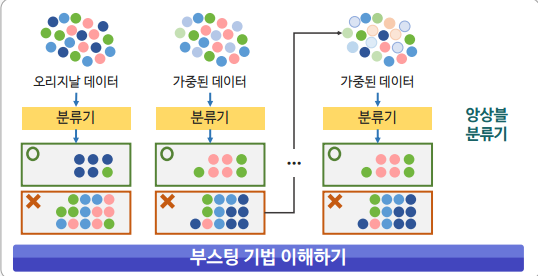
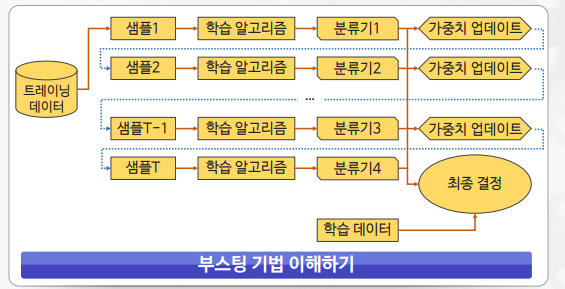
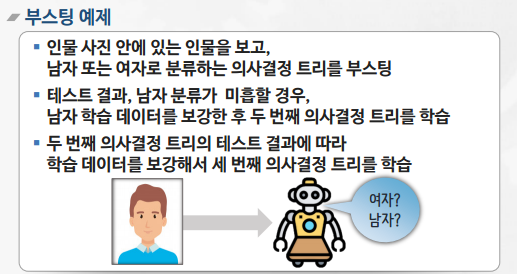
부스팅(Boosting)
- 이전 분류기의 학습 결과를 바탕으로 다음 분류기의 학습 데이터의 샘플 가중치를 조정하여 학습하는 방법
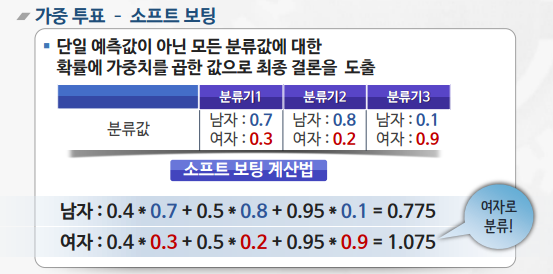
- 동일한 알고리즘의 분류기를 순차적으로 학습해서 여러 개의 분류기를 만든 후, 테스트할 때 가중 투표를 통해 예측값을 결정
- 대표적 모델 : XGBoost와 AdaBoost, GradientBoost

비지도 학습
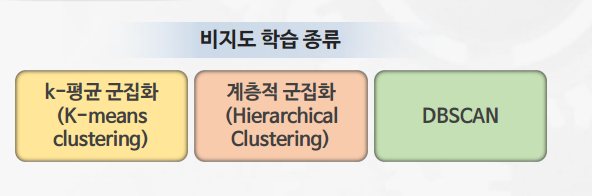
K-means 클러스터링
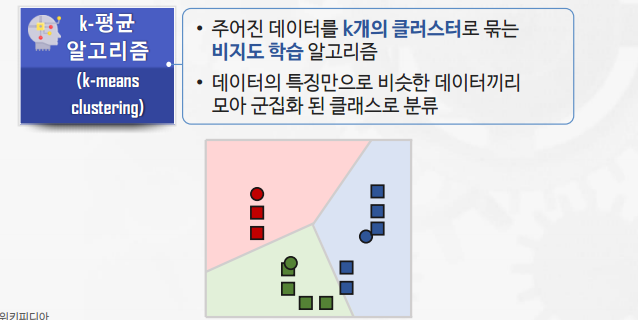
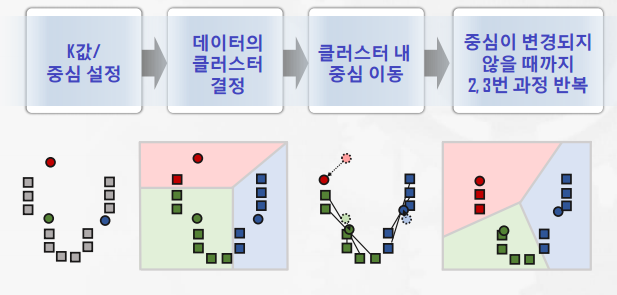
장점
- 간단한 알고리즘으로 구현이 용이
- 계산 시간이 비교적 짧음(속도가 빠름)
단점
- 초기 클러스터 개수와 중심에 따라 결과가 크게 달라질 수 있음
- 결과 해석이 쉽지 않음
계층적 군집화(Hierarchical Clustering)



댓글남기기